为什么测量效率时功率因数很重要？

功率因数和能效基础知识

使用外接电源（EPS）的工程师对效率测量并不陌生。但是，由于其应用通常采用直流电源运行，在测量电源交流侧的功率时可能会出现常见错误。这些常见陷阱包括在计算输入到电源的功率时错误地测量或完全忽略功率因数，从而导致效率测量结果不正确。在这篇博文中，我们将回顾功率因数和效率的基础知识，然后就如何在测量AC-DC电源效率时纳入功率因数测量提供指导。

功率因数和效率回顾

效率（η）是输出功率与输入功率的比率：

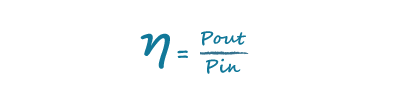
对于供应直流电的外接电源(EPS)，只需将输出电压乘以输出电流，即可快速得出方程式的分子，从而计算输出功率。

计算输出功率

计算直流EPS的输出功率，就是用输出电压乘以输出电流：

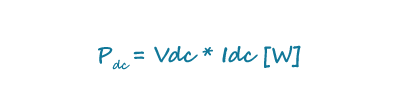
方程式2通过将输出电压(V_dc)乘以输出电流(I_dc)计算电源(EPS)的直流(dc)输出功率(P_dc)，从而得到以瓦特(W)为单位的功率。

了解功率因数

一个常见的错误就是采用同一计算方法求得输入功率。这就产生了一个问题，因为交流电路中的伏安乘积并不总是等于有功功率，事实上，在使用外接适配器时，伏安乘积永远不会等于有功功率。在交流电路中，伏安乘积等于视在功率(S)，视在功率通过功率因数(PF)与实际功率关联：

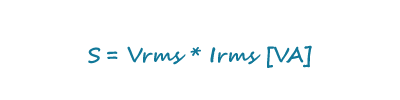
方程式3通过将均方根(rms)电压(Vrms)乘以均方根电流(Irms)，计算以伏安(VA)为单位的视在功率(S)。

定义功率因数

根据定义，功率因数是有功功率与视在功率的比值，其中视在功率是有效电压和有效电流的乘积。只有当功率因数等于1时，伏安乘积才等于有功功率：

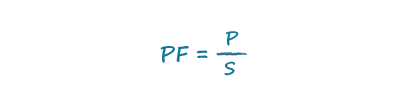
不同类型的功率因数

如果在计算效率时考虑功率因数，则必须正确计算该因数。许多工程师不得不一直回到他们早期学习的工程课程，才能想起功率因数是什么，以及如何测量它。然而，他们在学校时经常关注线性情况，此时的电压和电流都是频率相同的纯正弦曲线。在这种情况下，功率因数仅仅是电压和电流之间的相位差的余弦值，更准确地说，是位移功率因数：

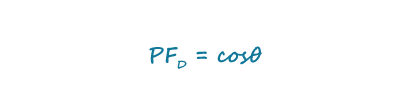
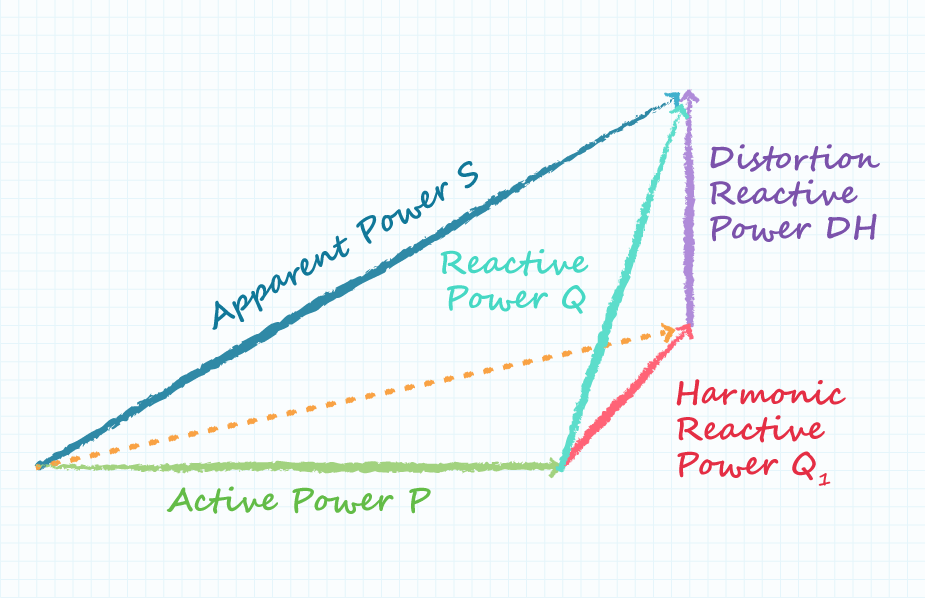
许多工程师都熟悉图1所示的功率三角形，它直观地表示了公式5的关系。根据定义，θ的余弦等于相邻边与斜边的比率。在功率三角形中，该值等于有功功率与视在功率的比值，这与我们在公式4中的定义相符。另一方面，在非线性系统中（AC-DC电源就是一个例子），这并不能代表所有情况。

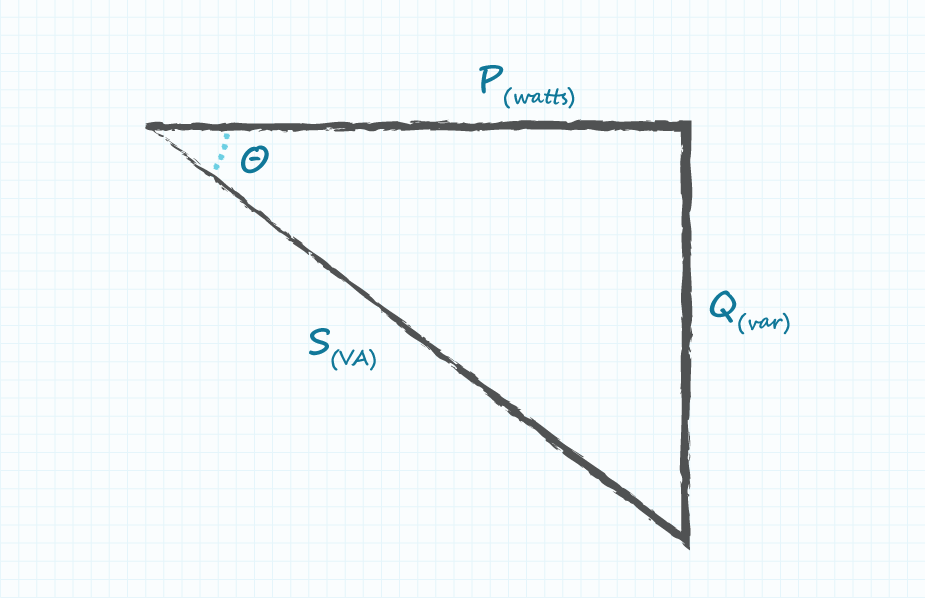
失真功率因数的作用

缺少的是失真功率因数，如图2所示，它为功率三角形增加了第三个维度。这一点至关重要，因为在电源中，失真因数是降低功率因数的主要原因，因为位移因数往往接近于1。

总谐波失真

傅立叶分析表明，这种非线性电流波形可以分解为一系列不同量级的谐波分量。这些谐波降低了功率因数，但未在公式5中计入。为计算失真功率因数，引入总谐波失真（THD）。THD考虑了与每个谐波相关的电流，如下面公式所示：

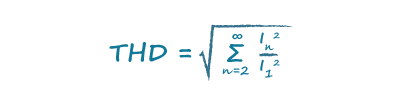
计算失真功率因数

当THD等于0时，失真功率因数等于1，线性系统就是这种情况：

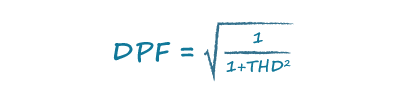
实际功率因数

功率因数通过乘以位移功率因数和失真功率因数来完成，从而求得有功功率因数：

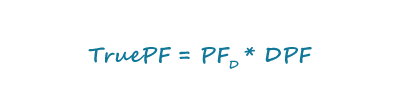
图3显示了典型电源的输入电流和电压波形。对比正弦电压，可以清楚地看到电流的非线性特性。

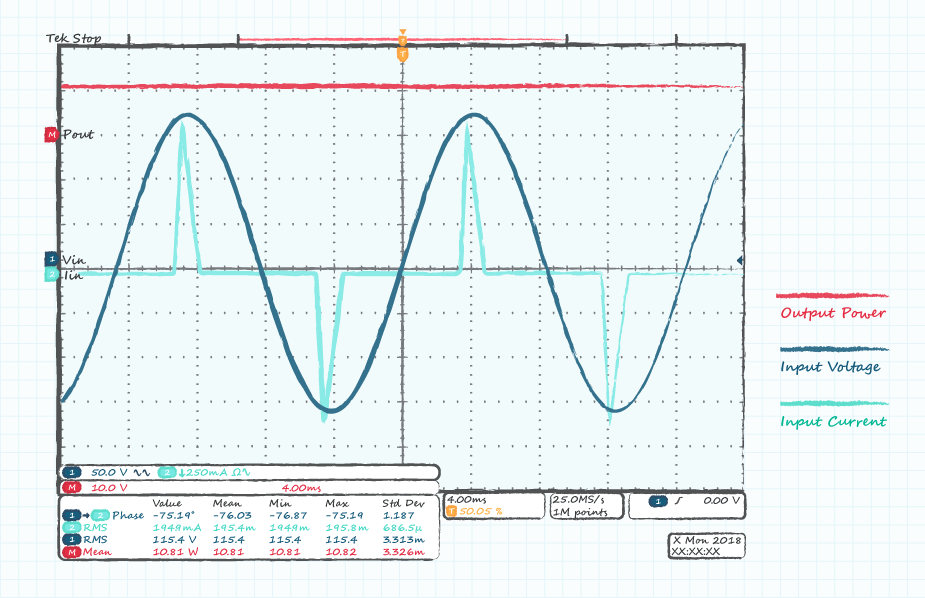
这是由桥式整流器和大容量电容器组合在电源内部形成高压直流母线造成的。整流器正向偏置，并且只有当输入电压超过大容量电容器上的电压时才会导通。

测量功率因数

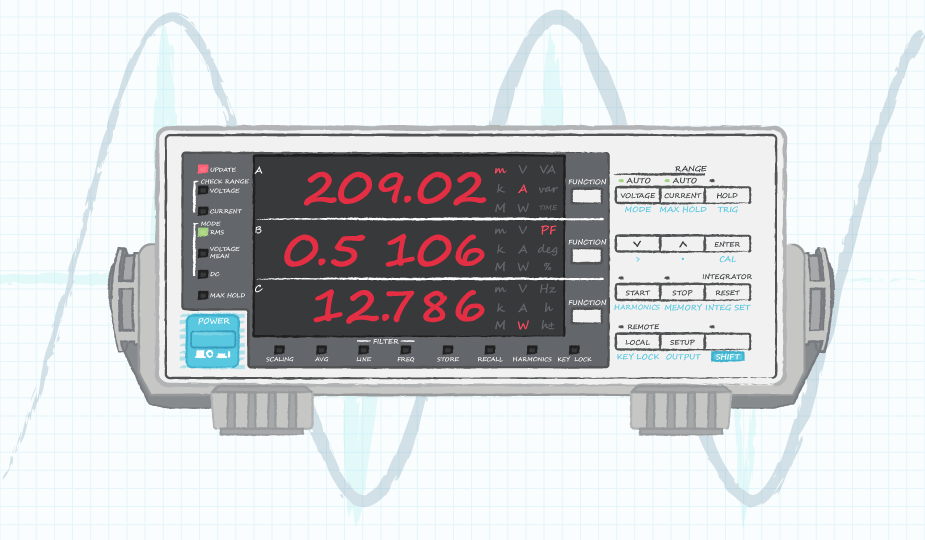
测量功率因数最好的方法是使用如下图4所示的功率计。这些设备将直接输出有功功率，因此在计算效率时不需要考虑功率因数。除了有功功率之外，这些仪表还可以测量每个谐波的功率因数、THD、电流等等。虽然低功率外接适配器没有明确的功率因数或谐波限制，但较高的电源对谐波含量和功率因数确实具有特定的监管限制。EN 61000-3-2等标准规定了一些功率等级中第39谐波以内的谐波电流的限值。测量电源的谐波电流时，功率计是必不可少的。

电源的功率因数

您可能会认为忽略功率因数的影响只会导致轻微的错误，而且/或者外接适配器的功率因数不会太差。实际上，如果没有功率因数校正，外接适配器的功率因数在额定负载下可能会低至0.5。功率因数为0.5的适配器的视在功率是有功功率的两倍，因此导致结果不正确。即使电源的实际效率为100%，该测量值也只会显示50%。

除了效率计划一律包含功率因数之外，务必要注意功率因数取决于线路和负载。效率要求（如美国能源部六级标准）要求在高、低线路电压下的几个点（25%、50%、75%和100%负载）测量效率。如果在计算有功功率时使用功率因数，则必须逐个重新测量这些条件。

实例：功率因数的影响

参考图3和图4中的实例，它们是从按照10.8 W运行的20 W外接电源中获得的。根据图3中的示波器测量得到的结果，我们得到的伏安乘积为22.5 VA。如果忘记纳入功率因数，那么使用这个数字我们将求得48%的效率得数：

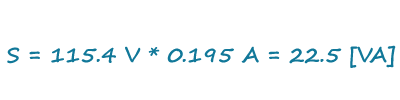
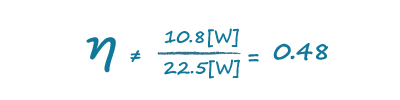
利用图4所示的功率计，我们可以看到有功输入功率实际上只有12.8 W，使用这个值我们最终求得84%的效率，这几乎是我们在不考虑功率因数时所得效率的两倍：

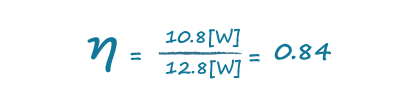
现在，如果考虑功率因数，但使用示波器和公式5来计算它（忽略失真因数），则会出现一些问题。首先，如图3所示，示波器可能难以自动计算相位差。图3中使用的示波器计算了72度的相位角，以肉眼观察，这似乎是不正确的。当使用示波器光标手动测量相位角时，我们注意到我们正试图测量两个不同形状的波形的偏移量，并且电流波形脉冲是不对称的。

那么问题来了：我们将光标放在哪里，在脉冲的高峰还是中心？无论哪种情况，该值最多都只有几度。如果我们使用公式5来计算角度为5°的位移功率因数，我们最终得到的值为0.996。如果我们将上面求得的22.5 VA的结果乘以计算得出的功率因数，就会发现结果几乎保持22.4 VA不变。这应该证实我们先前的说法，即位移因数接近于1，且失真功率因数是公式8中的主导项。因此，我们可以看到示波器方法对我们来说没有用处，而求得正确结果的唯一方法是使用功率计。

用于精确能效测试的功率计

几十年来日趋严格的监管使效率测试成为选择和验证电源的最重要因素之一。测试工程师如果缺乏处理交流电路的经验，就会忽略或错误地计算功率因数，导致求得不正确的效率得数。在测试外接适配器或任何AC-DC电源时，计算有功功率输入最好的方法就是使用功率计。这些设备不仅可以直接测量有功功率，还可以测量各个谐波的相关电流，并提供电源输入的完整图形。

类别： 基础知识，测试和故障分析

您可能还喜欢

功率范围为 1 W 至 550 W 的交流-直流电源

特色产品

功率因数和功率因数校正

应用注释

如何测量电源的纹波和瞬态

电源专题博客

针对本文章或您希望我们将来探讨的主题发表见解？
发送电子邮件至 powerblog@cui.com